О проекте
Курсы
Публикации
Контакты
ЛИЧНЫЙ КАБИНЕТ
Логотип Structuristik
Подкаст
Акции
PlayCAD
Подпишитесь на наши новости
Close
ПОДПИСКА НА НОВОСТИ STRUCTURISTIK
Даю согласие на обработку персональных данных.
СКИДКА 20% ЗА РЕШЕНИЕ ЗАДАЧИ
Получить
Устойчивость центрально сжатых стержней
СП 16.13330.2017
Один из самых «заезженных» расчетов стальных конструкций — устойчивость центрально сжатых стержней. Сам расчет со всеми указаниями изложен п. 7.1.3. Как думаете, сможем ли мы рассказать Вам что-нибудь новое, чего вы ещё не знали? Ну мы попробуем)
Условие устойчивости по п. 7.1.3 СП 16.13 330.2017 выглядит так:
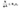
где N - сила сжатия
φ - коэффициент устойчивости при центральном сжатии
A - площадь поперечного сечения брутто
Ry - расчетное сопротивление стали по пределу текучести
γс - коэффициент условий работы.
Если со всеми участниками этой формулы все просто, то вот коэффициент φ хранит в себе несколько секретов. Согласно формуле (8) коэффициент φ определяется по формуле:
где δ - коэффициент
λ - условная гибкость стержня.
Коэффициент δ определяется по формуле:
α и β - коэффициенты, определяемые по таблице
λ - условная гибкость стержня.
Рисунок 1 — Таблица с типами сечений
При этом значение коэффициента φ не может превышать 1, и при гибкостях 3.8, 4.4 и 5.8 и значение коэффициента φ следует принимать не более:
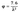
где λ - условная гибкость стержня.
Отлично, положения сводов правил мы повторили. Пора переходить к самому интересному.
Бифуркационная теория
Слово то какое страшное. Всю теорию рассказывать не буду, она уже рассказана тут. Я же приведу только самую выжимку.
Критическая сила по Эйлеру:
где Ncr - критическая сила потери устойчивости
E - модуль упругости стали
I - момент инерции стержня
μ - коэффициент расчетной длины
l - фактическая длина стержня
φ - коэффициент устойчивости при центральном сжатии
Ry - расчетное сопротивление стали по пределу текучести
A - площадь поперечного сечения стержня.
Выразим коэффициент устойчивости при центральном сжатии:
где E - модуль упругости стали
I - момент инерции стержня
μ - коэффициент расчетной длины
l - фактическая длина стержня
φ - коэффициент устойчивости при центральном сжатии
Ry - расчетное сопротивление стали по пределу текучести
A - площадь поперечного сечения стержня.
Вспомним формулу определения радиуса инерции сечении:
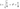
где i - радиус инерции сечения
I - момент инерции стержня
A - площадь поперечного сечения стержня.
Подставим в формулу выше и получим:
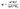
Что-то в этой формуле кажется знакомым, а — гибкость:
где λ - гибкость стержня
μ - коэффициент расчетной длины
l - фактическая длина стержня
i - радиус инерции стержня.
Подставим и это в формулу:
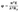
где E - модуль упругости стали
λ - гибкость стержня
Ry - расчетное сопротивление стали по пределу текучести.
Кажется есть еще один способ упростить:
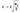
где λ - гибкость стержня
Ry - расчетное сопротивление стали по пределу текучести
E - модуль упругости стали.
Подставим и получим:
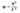
где λ - гибкость стержня.
Давайте посмотрим как будет выглядеть график коэффициента устойчивости.
Рисунок 2 — Коэффициент устойчивости при центральном сжатии стержней по бифуркационной теории
Однако такое точное решение подойдет только для идеально прямых стержней, а вот для реальных стержней, хотелось бы сделать небольшой коэффициент запаса, иначе при нагружении они могут сильно деформироваться в сторону еще до достижения предельной нагрузки. Построим график для коэффициента устойчивости с учетом коэффициента запаса устойчивости γs=1.3.
Рисунок 3 — Коэффициент устойчивости при центральном сжатии стержней по бифуркационной теории с учетом коэффициента запаса устойчивости
Судя по графикам, коэффициент устойчивости равен 1 при условной гибкости 3.14 без учета коэффициента запаса устойчивости и 2.75 с учетом коэффициента запаса устойчивости. Окей, теперь пришло время поговорить про деформационную теорию устойчивости.
Деформационная теория
Если вкратце: деформационная теория основана на придании стержню некоторого начального несовершенства в виде искривления или приложения сжимающей силы с эксцентриситетом и определения внешней силы, при которой в крайнем волокне стержня наступает текучесть при его изгибе по кривой, описываемой формой синусоиды.
Пропускаем все зубодробительные вычисления и посмотрим только на решения. Строгое решение имеет вид:
где δ - коэффициент, характеризующий начальное несовершенство
λv - условная гибкость стержня, с учетом относительного эксцентриситета.
Коэффициент δ определяется по формуле:
где m0 - относительный эксцентриситет
λ - условная гибкость стержня.
Условная гибкость стержня определяется по формуле:
где λ - условная гибкость стержня, m0 - относительный эксцентриситет.
Не строгое решение имеет знакомый нам вид:
где δ - коэффициент, характеризующий начальное несовершенство
λ - условная гибкость стержня.
Коэффициент δ определяется по формуле:
где m0 - относительный эксцентриситет
λ - условная гибкость стержня.
Нормативная методикА
Как Вы поняли, наши нормы предлагают пользоваться нестрогим решением. Построим графики коэффициентов устойчивости для всех трех типов сечений и для решения по бифуркационной теории.
Рисунок 4 — Графики коэффициента устойчивости при нестрогом решении.
Видно, что кривая полученная с учетом коэффициента запаса по бифуркационной теории пересекает кривые для типов сечения a, b и с полученные по деформационной теории при гибкостях 3.74, 4.39 и 5.71 соответственно. Что очень похоже на коэффициенты 3.8, 4.4 и 5.8 для типов сечений a, b и c соответственно в наших нормах, при которых следует определять коэффициент устойчивости по формуле:
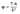
где λ - условная гибкость стержня.
Думаю Вы уже поняли, что это за 7.6, если нет, то:
где γs — коэффициент запаса устойчивости.
Таким образом, вместо установления границ перехода от одного метода расчета к другому коэффициент устойчивости при центральном сжатии φ следует принимать как меньшее из полученного по бифуркационной и деформационной теориям. Таким образом графики значений коэффициентов устойчивости по СП будут иметь вид:
Рисунок 5 — Графики коэффициента устойчивости при нестрогом решении с учетом бифуркационной теории.
Давайте теперь построим графики значений коэффициентов устойчивости при строгом и нестрогом решениям. Относительный эксцентриситет определим по методике СП 16.13 330.2017.
где α и β - коэффициенты, в зависимости от типа сечения.
Тогда для сечений типа a, b и c графики значений коэффициентов устойчивости при центральном сжатии φ в зависимости от условной гибкости стержня будет иметь вид, представленный на рисунке 6.

Рисунок 6 — Значение коэффициента устойчивости при строгом (пунктир) и нестрогом (сплошная) решениях.

Как видно при нестрогом решении коэффициент устойчивости оказывается выше, чем при строгом. Построим график отношения переоценки несущей способности СП по отношению к строгому решению для всех трех типов сечений.

Рисунок 7 — Переоценка несущей способности при нестрогом решении.

Видно, что применение нестрогого решения приводит к завышению несущей способности центрально сжатого стержня для всех трех типов сечений в наиболее часто применяемом диапазоне условных гибкостей. Превышение составляет порядка 3%, 3.5% и 4% для типов сечения a, b и c. Не то чтобы это были какие-то серьезные цифры, но о них стоит помнить особенно в тех случаях когда вы проектируете центрально сжатые элементы загруженные преимущественно постоянной нагрузкой под коэффициент использования 0.999.
Типы сечений
СП 16.13 330.2017 не содержит никаких критериев отнесения сечений к одному из типов, кроме данных, представленных в таблице 7. Таким образом, при проектировании составного сечения, которое не приведено в таблице 7 СП 16.13 330.2017 проектировщик оказывается в затруднительном положении и вынужден принимать худший вариант (тип c) в запас.
Согласно указаниям Ю. В. Соболева отношение сечения к определенному типу производится на основании параметра Ω, определяемого по формуле:
где e0 - эксцентриситет
m0 - относительный эксцентриситет
i - радиус инерции сечения
W - момент сопротивления сечения
A - площадь поперечного сечения
I - момент инерции сечения.
При попадании параметра Ω в диапазон от ⅔ до 1 сечения следует относить к типу а, при попадании в диапазон от 0.4 до ⅔ - к типу b, в остальных случаях к типу c. Обратите внимание, что для каждой плоскости тип сечения следует определять отдельно.

Проанализировав по такому критерию двутавры по ГОСТ Р 57 837−2017 обнаружим, что в плоскости x-x все двутавры следует относить к типу сечений а, а в плоскости y-y все, кроме 60ДБ1 и 60ДБ2, к типу сечений b. Двутавры 60ДБ1 и 60ДБ2 в плоскости y-y следует относить к типу сечений c.
Уточнение методики
Таким образом не сложно представить уточненную нормативную методику с учетом строгого решения и критерия типа сечения.
Коэффициент Ω следует определять по формуле:
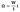
Случайный относительный эксцентриситет следует определять по формуле:
Коэффициенты α и β принимать в зависимости от типа сечения, по таблице:
Коэффициент, учитывающий начальное несовершенство следует определять по формуле:
Коэффициент, учитывающий поворот оси стержня на концах, следует определять по формуле:
Коэффициент устойчивости при центральном сжатии следует определять по формуле:
Изложенная методика упростит восприятие и даст строгое деформационное решение. Окончательные кривые для типов сечений a, b и c имеют вид.

Рисунок 8 — Зависимость значений коэффициентов устойчивости от условной гибкости по уточненной методике.

ВЫВОД
Мы разобрались, в логике работы нормативной методики, установили природу применяемых в нормативной методике числовых и буквенных коэффициентов. Определили метод определения типа сечения, для сечений не представленных в таблице 7 СП 16.13 330.2017. И сформировали методику определения более точных коэффициентов устойчивости центрально сжатых стержней.
Если остались вопросы — пишите их нам в социальных сетях.


Автор статьи:

Блинов Сергей

Инженер-конструктор

ПУБЛИКАЦИИ