О проекте
Курсы
Публикации
Контакты
ЛИЧНЫЙ КАБИНЕТ
Логотип Structuristik
Подкаст
Акции
PlayCAD
Подпишитесь на наши новости
Close
ПОДПИСКА НА НОВОСТИ STRUCTURISTIK
Даю согласие на обработку персональных данных.
СКИДКА 20% ЗА РЕШЕНИЕ ЗАДАЧИ
Получить
Расчет фундаментных болтов
Введение
Проектирование анкерных креплений оборудования и закладных уже несколько лет в нашей стране выполняется по обновленной методике, а проектирование баз стальных колонн продолжают выполнять по старой. В этой статье разберемся с этими методиками и рассмотрим как считать фундаментные болты по ГОСТ по новой методике. Сразу скажу, что в этот раз мы говорим только о проверках по стали болтов. Конечно, проверки по бетону очень и очень важны, но о них мы рассказывали в курсе Мастер узлов.
Определяем расчетное сопротивление
СП 16.13330.2017
Мы привыкли, что все что касается расчета стальных конструкций сведено в СП 16.13 330 и СП 294.1 325 800. Расчет болтов по общим правилам выполняется в соответствии с разделом 14.2 СП 16.13 330.2017. Однако пункт 14.2.15 СП 16.13 330.2017 гласит:
Фундаментные (анкерные) болты следует проверять согласно требованиям СП 43.13 330.
Таким образом расчет фундаментных болтов, согласно СП 16.13 330.2017 следует выполнять по СП 43.13 330.2012. Однако, задачу определения расчетных сопротивлений фундаментных болтов СП 16.13 330.2017 берет на себя. Пункт 6.6 гласит:
Расчетное сопротивление растяжению фундаментных и анкерных болтов Rba следует определять по формуле:
Значения расчетных сопротивления растяжению фундаментных болтов приведены в таблице Г. 7 (Приложение Г).
Таблица 1 — Расчетные сопротивления растяжению фундаментных болтов по таблице Г. 7 СП 16.13 330.2017
Диаметр болтаРасчетные сопротивления Rba, МПа, болтов из стали: Ст3пс4, Ст3пс2, Ст3сп4, Стсп2Расчетные сопротивления Rba, МПа, болтов из стали: 09Г2С-4, 09Г2С-6
M16200265
M20200265
M24190245
M30190245
M36190230
M42180230
M48180230
M56180230
M64180230
У конструкторов с опытом начинают закрадываться первые сомнения. Вроде раньше значения были другими. Давайте первым делом заглянем в СНиП II.23−81. Расчетные сопротивления растяжению фундаментных болтов приведены в таблице 60* СНиП II.23−81*.

Таблица 2 — Расчетные сопротивления растяжению фундаментных болтов по таблице 60* СНиП II.23−81
Диаметр болтаРасчетные сопротивления Rba, МПа, болтов из стали: ВСт3кп2Расчетные сопротивления Rba, МПа, болтов из стали: 09Г2СРасчетные сопротивления Rba, МПа, болтов из стали: 10Г2С1
M16145185190
M20145185190
M24145185190
M30145185190
M36145180180
M48145180180
M56145180180
M64145175170
Видим, что значения сильно отличаются. Заглянем в раздел 3 СНиП II-23−81* и найдем пункт 3.6:

3.6*. Расчетное сопротивление растяжению фундаментных болтов Rba следует определять по формуле:
Ага, формулу определения расчетного сопротивления растяжению изменили. Чем же обоснованы подобные изменения? В поисках ответа я наткнулся на статью В. М. Горпинченко, В. И. Патыка и А. В. Паршина (ЦНИИСК им. Кучеренко) «Исследование прочности фундаментных болтов» в журнале «Строительная механика и расчет сооружений» 1988 года. В статье утверждается что на расчетную прочность фундаментных болтов влияют факторы:
  • возможная перегрузка смежных болтов в результате неравномерной их затяжки;
  • внецентренное нагружение болта из-за наличия в соединении перекосов опорных элементов;
  • присутствие резкого концентратора напряжений в виде канавки резьбы.

Приведу краткие выдержки из статьи:

…По результатам испытаний установлено, что как для малоуглеродистой, так и для низколегированной стали наличие концентратора в виде канавки резьбы приводит к повышению пределов текучести и прочности соответственно на 18.20 и 10%…

…Полученные разрушающие напряжения показали, что увеличения угла перекоса с 0° до 25° приводит к снижению несущей способности фундаментных болтов на 10%…

…В перечисленных соединениях неравномерность затяжки болтов приводит к снижению несущей способности соединения на 10%…

…Для образования жесткого сопряжения конструкций с фундаментом используют болты, которые должны воспринимать расчетный изгибающий момент. Это возможно только в том случае, если материал анкерного болта будет работать в упругой стадии. Очевидно, что в этом случае при установлении расчетных сопротивлений необходимо основываться на пределе текучести материала фундаментных болтов…

На основании полученных данных авторы предлагают следующую формулу для определения расчетного сопротивления фундаментных болтов растяжению:
где Run – нормативное сопротивление стали болта по пределу прочности
K – коэффициент, учитывающий соотношение пределов текучести Ryn и прочности стали Run
γ1с=0.9 – коэффициент, учитывающий снижение несущей способности многоболтового соединения, вследствие неравномерной затяжки смежных болтов
γ2с=0.9 – коэффициент, учитывающий снижение несущей способности болта при перекосах
γ3с=1.15 – коэффициент, учитывающий превышение несущей способности болта над несущей способностью гладкого образца в результате концентрации напряжений
γm – коэффициент надежности по материалу фундаментного болта;

По таблице 2 и таблице 51 найдем значения коэффициентов γm и K и подставим в уравнение. Тогда:
  • для малоуглеродистых сталей
  • для низколегированных сталей
Из чего авторы рекомендуют принять в нормах следующую формулу для определения расчетных сопротивлений фундаментных болтов растяжению:
Таким образом, автором предложено повысить расчетное сопротивление фундаментных болтов растяжению на 25%, по сравнению со СНиП II.23−81*. Это объясняет изменение формулы определения расчетного сопротивления стали фундаментных болтов в СП 16.13 330.2017 по сравнению со СНиП II.23−81*.

Избавившись от перехода от предела текучести к пределу прочности с помощью коэффициента K получим:
Или, с учетом актуального значения коэффициента надежности по материалу согласно таблице 3 СП 16.13 330.2017 изм.2 для проката без статистической процедуры контроля свойств:
Видно, что расчетное сопротивление фундаментных болтов растяжению по методике предложенной В. М. Горпиченко, В. И. Патыкой и А. М. Паршиным по результатам исследований превышает указанное в СП 16.13 330.2017 на 12.5%.
ГОСТ 24379.0-2012
Согласно таблице 1 ГОСТ 24 379.0−2012 «Болты фундаментные. Общие технические условия» шпильки фундаментных болтов изготавливаются из стали марок:
  • Ст3кп, Ст3пс и Ст3сп по ГОСТ 535–2005;
  • 20 по ГОСТ 1050–2013
  • 09Г2С и 10Г2С1 по ГОСТ 19 281–2014
Ни таблица Г. 7 СП 16.13 330.2017, ни таблица 60* СНиП II.23−81* не содержат табличных данных по расчетному сопротивлению фундаментных болтов всех марок стали, из которых изготавливают болты. Пробежимся по ГОСТам и вычислим расчетные сопротивления для фундаментных болтов.
Начнем с ГОСТ 535–2005 «Прокат сортовой и фасонный из стали углеродистой обыкновенного качества. Общие технические условия». Нормативный предел текучести стали зависит от марки стали и толщины проката. Все данные сведем в таблице.

Таблица 3 — Расчетные сопротивления стали фундаментных болтов растяжению из сталей марок Ст3кп, Ст3пс и Ст3сп
БолтСт3кп (1)Ст3кп (2)Ст3кп (3)Ст3кп (4)Ст3пс (1)Ст3пс (2)Ст3пс (3)Ст3пс (4)Ст3сп (1)Ст3сп (2)Ст3сп (3)Ст3сп (4)
M16235-188211.5245200196220.5245200196220.5
M20235-188211.5245200196220.5245200196220.5
M24225-180202.5235190188211.5235190188211.5
M30225-180202.5235190188211.5235190188211.5
M36225-180202.5235190188211.5235190188211.5
M42215-172193.5225180180202.5225180180202.5
M48215-172193.5225180180202.5225180180202.5
M56215-172193.5225180180202.5225180180202.5
M64215-172193.5225180180202.5225180180202.5
(1) Нормативный предел текучести σт по таблице 2 ГОСТ 535-2005;
(2) Расчетное сопротивления фундаментного болта растяжению по таблице Г.7 СП 16;
(3) Расчетное сопротивление фундаментного болта растяжению по формуле (1) СП 16;
(4) Расчетное сопротивление фундаментного болта растяжению по результатам исследования.
Видно, что данные таблицы Г. 7 СП 16.13 330.2017 хорошо совпадают со значениями, полученными по формуле (1) СП 16.13 330.2017.
Перейдем к ГОСТ 1050–2013 «Металлопродукция из нелегированных конструкционных качественных и специальных сталей». Нормативный предел текучести стали зависит только от марки стали и не зависит от толщины проката. Данные сведены в таблицу.

Таблица 4 — Расчетные сопротивления стали фундаментных болтов из стали марки 20
Болт20 (1)20 (2)20 (3)20 (4)
M16-M64245-196220.5
(1) Нормативный предел текучести σт по таблице 4 ГОСТ 1050-2013;
(2) Расчетное сопротивления фундаментного болта растяжению по таблице Г.7 СП 16;
(3) Расчетное сопротивление фундаментного болта растяжению по формуле (1) СП 16;
(4) Расчетное сопротивление фундаментного болта растяжению по результатам исследования.
Увы, но сравнивать результаты нам просто не с чем. Да и закладывают болты из качественной конструкционной стали не часто. Так что больше просто к сведению.
Завершает марафон табличек ГОСТ 19 281–2014 «Прокат повышенной прочности. Общие технические условия». И вот тут нас ждет сюрприз. Согласно ГОСТ нормативный предел текучести стали не зависит ни от марки стали, ни от толщины проката, а только от класса прочности. Данные в таблице.

Таблица 5 — Расчетные сопротивления стали фундаментных болтов из стали марок 09Г2С и 10Г2С1
Класс прочности09Г2С и 10Г2С1 (1)09Г2С и 10Г2С1 (2)09Г2С и 10Г2С1 (3)09Г2С и 10Г2С1 (4)
265260265-220212238,5
295295265-220236265,5
315315265-220252283,5
325325265-220260292,5
345345265-220275310,5
355355265-220284319,5
375375265-230300337,5
390390265-230312351
(1) Нормативный предел текучести σт по таблице 2 ГОСТ 19281-2014;
(2) Расчетное сопротивления фундаментного болта растяжению по таблице Г.7 СП 16;
(3) Расчетное сопротивление фундаментного болта растяжению по формуле (1) СП 16;
(4) Расчетное сопротивление фундаментного болта растяжению по результатам исследования.
Видно, что данные таблицы Г. 7 СП 16.13 330.2017 совершенно не соответствуют ГОСТ. Как же тогда они были получены? Может быть в предыдущей редакции ГОСТ 19 281–89 нормативный предел текучести зависел от толщины и марки? Нет. Уже в ГОСТ 19 281–89 были введены классы прочности проката, а вот в ГОСТ 19 281–73 нормативный предел текучести проката зависел от толщины проката и марки стали. Логично предположить, что данные таблицы 60* в СНиП II.23−81* основывались на действовавшем на тот момент ГОСТ 19 281–73. А вот в СП 16.13 330.2017 перекочевали просто по наследству без актуализации. Так что при заказе фундаментных болтов не забывайте указать класс прочности стали, если закладываете болты из сталей 09Г2С и 10Г2С1, иначе на площадку вам могут привезти болты с прочностью ниже, чем вы рассчитывали.
Хорошо, теперь разобрались. Формально выполняем требования СП 16.13 330.2017 с формулой (1), но значения Ryn подставляем в зависимости от стандарта на сталь, марки стали, толщины проката и класса прочности.
Разбираемся с определением усилий в болтах от нормальной силы и момента
СП 43.13 330.2012
Переходим к определению усилий в болтах. Расчет анкерных болтов для креплений конструкций и оборудования сведен в приложение Г СП 43.13 330.2012. По началу все просто, первые вопросы начинаются вместе с пунктом Г.12

При групповой установке болтов для крепления оборудования значение расчетной нагрузки P, приходящейся на один болт, следует определять для наиболее нагруженного болта:
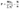
где M – расчетный изгибающий момент
y1 – расстояние от оси поворота до наиболее удаленного болта в растянутой зоне стыка
yi – расстояние от оси поворота до i-того болта, при этом учитываются как растянутые, так и сжатые болты
N – расчетная продольная сила
n – общее число болтов.
Эта формула справедлива, только если предположить, что всё держиться только на болтах и никакого бетона под «лапами» и опорными плитами оборудования просто нет, все болты имеют одинаковую площадь поперечного сечения. Иначе, применять эту формулу нельзя. В этом же пункте есть ещё одно примечание:

Ось поворота допускается принимать проходящей через центр тяжести опорной поверхности оборудования или башмака колонн.

Такое тоже можно допускать не всегда. Вернее это можно допускать только тогда когда центр тяжести группы болтов совпадает с центром тяжести опорной поверхности, а иначе это приведет к недооценке усилия в наиболее удаленном от центра поворота болте. Далее встречаем пункт Г.14:

Для башмаков стальных сплошных колонн значение расчетной нагрузки, приходящейся на один растянутый болт, следует определять по формуле:
где Rb – расчетное сопротивление бетона осевому сжатию
bs – ширина опорной плиты башмака
x – высота сжатой зоны бетона под опорной плитой башмака, определяемая по СП 63.13330, как для внецентренно сжатых элементов
N – расчетная продольная сила в колонне
n – число растянутых болтов, расположенных с одной стороны башмака колонны.
Не сложно догадаться, что это формула получена из решения уравнения равновесия всех сил относительно вертикальной оси:
Вот только решение такое действительно, только если все растянутые болты нагружены равномерно, а происходит это если все растянутые болты равноудалены от оси поворота. Правда, об этом, почему-то забыли упомянуть. Поэтому если болты у Вас расположены в несколько рядов (по групповой установке), то применение этой формулы приведет к тому, что в наиболее удаленных болтах усилия достигнут предела текучести и деформации соединения начнут стремительно развиваться, что в свою очередь, приведет к повышению податливости соединения.

Таким образом СП 43.13 330.2012 ставит нас в тупик. Или ставить все болты на одинаковом расстоянии от точки поворота и применять одну формулу или ставить их как удобно, но исключать из работы бетон.
Думаю, Вы уже догадались, что применить положения СП 63.13 330.2018 относительно внецентренно сжатых элементов к определению высоты сжатой зоны бетона под опорной плитой башмака будет той ещё задачкой. При относительный высоте сжатой зоны бетона не более граничной высоты сжатой зоны бетона по формуле:
При относительный высоте сжатой зоны бетона более граничной высоты сжатой зоны бетона по формуле:
Не знаю как Вам, а мне и одного вида этих формул хватает за глаза. Очевидно, что если нам повезет, высота сжатой зоны бетона окажется меньше граничной и расчет сойдется с первого раза, если нет, то желающему обеспечен итеративный расчет с последующими приближениями.
Есть способ попроще. Примем, что все растяжение воспринимают только болты крайнего ряда. Это допущение будет в запас прочности. И составим уравнение моментов вокруг оси равнодействующей в крайнем ряду болтов:
где N - сжатие в колонне
e – относительный эксцентриситет
y – расстояние от центра тяжести колонны до оси крайнего ряда болтов
q – давление под опорной плитой
x – высота сжатой зоны бетона
bs – размер плиты в направлении, перпендикулярном действию момента
h – размер плиты в направлении действия момента.
Вместо q подставим Rb, раскроем скобки и решим уравнение относительно высоты сжатой зоны:
Думаю, вы уже узнали в этой формуле ту самую формулу из Пособия к СНиП 2.09.03−85. Вот мы и установили её природу. Теперь можно воспользоваться формулой для определения усилия растяжения в одном фундаментном болте, только вместо количества болтов растянутой зоны подставить количество болтов крайнего ряда растянутой зоны. Такое решение будет справедливым.
Переходим к сдвигу
К сдвигу даже переходить страшно. Сам СП 43.13 330.2012 устанавливает только две формулы. Одну для сквозных колонн, другую для сплошных. Предельное сдвигающее усилие для сплошных колонн может быть определено по формуле:
где f=0.25 – коэффициент трения по интерфейсу сталь-бетон
n – количество болтов сжатой зоны
An – площадь сечения нетто фундаментного болта
Rba – расчетное сопротивление стали фундаментного болта растяжению
N – сжатие в колонне.
Ну со вторым слагаемым все понятно, это трение опорной плиты по бетону. А вот что такое первое? Судя по аннотации к формуле, это дополнительное прижатие опорной плиты от натяжения болтов. При этом в пособии к СНиП 2.09.03−93 имеется формула, по которой определяется требуемое натяжение. Увы, эта формула не перекочевала в приложение СП 43.13 330.2012. Однако, при учете вклада натяжения болтов в расчет принимается только четверть, от возможного. Никаких статей и пояснений я не нашел, так что остается предположить, что таким образом учтены потери первоначального натяжения при циклическом действии нагрузки и от ползучести бетона.
Чуть в сторону
Сделаем одно лирическое отступление. В СП 43.13 330.2012 есть формула определения минимальной глубины заделки фундаментных болтов в основание:
где H0 – базовая глубина заделки в зависимости от типа болта
m1 – отношение расчетного сопротивления растяжению бетона класса B12.5 к расчетному сопротивлению принятого бетона
m2 – отношение расчетного сопротивления растяжению металла болтов принятой марки стали к расчетному сопротивлению растяжению стали марки ВСт3кп2.
Все бы ничего, но ни СП 16 ни СП 43 не содержат расчетного сопротивления растяжению металла болтов из стали марки ВСт3кп2. И потому среди конструкторов встречаются разные подходы. Один из них — принять в качестве расчетного сопротивления растяжению металла болтов из стали марки ВСт3кп2 значение в 145 МПа, потому как именно это значение было указано в СН 417−75 и было правильным на момент действия СНиП II.23−81*. Однако так делать не правильно, так как действующая методика определения расчетного сопротивления отличается от методики СНиП II.23−81*. Следует сравнивать значения расчетных сопротивлений полученных по одной методике.
Часто, краевые расстояния и минимальная глубина заделки являются определяющими при назначении размеров фундаментов. СП 43.13 330.2012, Пособие к СНиП и СН 417−75 допускают только одно отступление:

Расстояние между болтами, а так же от оси болтов до грани фундамента допускается уменьшать на 2d при соответствующем увеличении глубины на 5d

Однако эти требования можно обоснованно нарушить, просто подтвердив это расчетом. И в курсе Мастер узлов мы очень подробно занимаемся разбором этих обоснований и тестируем все это на примерах. А теперь вернемся к нашему расчету.
Обратно к расчету
СП 513.1 325 800.2022
Относительно недавно вступил в силу свод правил СП 513.1 325 800.2022 «Анкерные крепления к бетону. Правила проектирования». Этот свод правил распространяется на проектирование анкерных креплений строительных конструкций и оборудования к бетонным и железобетонным конструкциям новых и реконструируемых зданий и устанавливает требования к расчету анкерных креплений с применением механических стальных, клеевых и комбинированных одиночных анкеров и групп анкеров (кроме пластиковых). Вроде подходит, правда СП не содержит определения термина «механический анкер», но ссылается на термины ГОСТ Р 57 787−2014, который уже содержит:

Механический анкер — анкер, в котором передача усилий на строительное основание с анкерного стержня осуществляется за счет сил трения или упора составных частей анкера с основанием.

Фундаментные болты являются механическими анкерами. Соответственно, положения нового свода правил распространяются на расчет фундаментных болтов. Это хороший и полноценный СП. В нем содержится методика проверки прочности анкерных креплений по стали на действие растяжения, сдвига и их совместное действие.
Рисунок 1 – Условия прочности механических анкеров при действии растягивающих усилий
по СП 513.1325800.2022.

Рисунок 2 – Условия прочности механических анкеров при сдвиге по СП 513.1325800.2022.

Но есть одна проблема: для выполнения всех расчетов нужен технический паспорт содержащий необходимые величины и коэффициенты. Как Вы уже догадались, на фундаментные болты по ГОСТ никто таких паспортов не делал. Эх, а счастье было близко.
ACI 318−19 и EN 1992−4
Мы были бы не мы, если бы не решили подглядеть у американцев. Заглядываем в ACI 318−19 и вот что видим:

Рисунок 3 – Условия прочности механических анкеров по ACI 318-19.

Те же самые формулы, только индексы другие. А в EN 1992−4?

Рисунок 4 – Условия прочности механических анкеров при действии растяжения по EN 1992-4.

Рисунок 5 – Условия прочности механических анкеров при сдвиге по EN 1992-4.

Не остается никаких сомнений, что ноги у всего этого растут из одного места. И точно, тут же в комментариях к ACI находим место роста ног) — Anchorage in Concrete Construction — R. Eligehausen, R. Malle, J.F.Silva — 2006. Огромная книга посвященная исследованиям, испытаниям и расчетам анкерных креплений. Тут же без особого труда находим формулы, по которым можно определить недостающие данные из технического паспорта:
Первоисточник
Нормативное значение силы сопротивления анкера при разрушении по стали от растяжения определяется по формуле:
где An – площадь поперечного сечения болта нетто
Rn – нормативное сопротивление стали анкера в зависимости от выполняемой проверки.
Нормативное значение силы сопротивления анкера при разрушении по стали от среза определяется по формуле:
где α – эмпирический коэффициент
A – площадь поперечного сечения анкера
Rn – нормативное сопротивление стали анкера в зависимости от выполняемой проверки.
Где W – момент сопротивления сечения анкера
Ryn – нормативное сопротивление стали анкера по пределу текучести.
Сравним формулы первоисточника с ACI 318-19 и EN 1992-4
Первоисточник
ACI 318-19
EN 1992-4
Я поменял обозначения в формулах, что бы читалось легче. Если вы загляните в документы, то увидите там другие обозначения, но при детальном рассмотрении, отследив всю цепочку сможете убедиться, что это тоже самое. Думаю тут всё понятно без слов.
Обратно на родину
Так, формулы есть, осталось только принять коэффициенты надежности соответственно нашим нормам и можно будет применять СП 513.1 325 800.2022. Пришлось долго поискать, но под руки всё же попалось пособие минстроя по проектированию закладных 2019 года выпуска. Там, как Вы уже догадались методика расчета анкеров и бетона применена для закладных. И, о чудо, никаких технических паспортов на арматуру делать, конечно-же не стали, и слава Богу.
Статья и так уже огромная, так что приведу формулы сразу с преобразованиями. Сразу отмечу, что согласно тексту пособия формулы применимы для клеевых химических анкеров со стальной арматурой А400-А500, выпускаемой по ГОСТ 5781 и ГОСТ Р 52 544.
Предельное растягивающее усилие из условий прочности по стали следует определять по формуле:
где Rsn – нормативное сопротивление арматурной стали растяжению
d – диаметр арматурного стержня
γNs=1.25 – коэффициент надежности по стали
As – площадь поперечного сечения арматурного стержня
N0.u.s – нормативное значение силы сопротивления анкера при разрушении по стали при растяжении.
Предельное значение силы сопротивление анкера по стали при сдвиге следует определять по формуле:
где 0.5 – эмпирический коэффициент, численное значение коэффициента α из первоисточника
Rsn – нормативное сопротивление арматурной стали растяжению
d – диаметр арматурного стержня
γVs=1.25 – коэффициент надежности по стали
As – площадь поперечного сечения арматурного стержня
Vu.s – нормативное значение силы сопротивления анкера при сдвиге.
Предельный изгибающий момент для анкера следует определять по формуле:
где 1.5 – эмпирический коэффициент первоисточника
Rsn – нормативное сопротивление арматурной стали растяжению
d – диаметр арматурного стержня
γVs=1.25 – коэффициент надежности по стали
W – момент сопротивления сечения анкера
Vu.s – нормативное значение силы сопротивления анкера при сдвиге.
Отлично, теперь у нас есть формулы и коэффициенты запаса. Остается один вопрос — область применимости. Формулы приведены для клеевых и механических анкеров из арматуры. То, что разницы между арматурой и стержнем фундаментного болта нет это лишь наше предположение и с этим предположением мы обратились к специалистам НИИЖБ. С нами связался Заведующий лабораторией самонапряженных конструкций и напрягающих бетонов НИИЖБ им. А. А. Гвоздева — Иванов Сергей Ильич.
Вопрос к данным, которые по СП 513.1 325 800.2022 нужно брать из технического паспорта. Я нашел пособие по закладным и там есть формулы для расчета для химических и механических анкеров из арматурных стержней. Там всё понятно, по ним можно посчитать и фундаментные болты. Вопрос только к коэффициентам надежности, которые там указаны. Можно ли их применять для фундаментных болтов?
СП 513.1325800.2022 не различают пост- и предустановленные анкеры. Эта часть расчета – целиком по стали, без всяких сомнений принимайте для фундаментных болтов.
Больше спасибо, специалистам НИИЖБ за оперативные ответы. Итак. Теперь у нас есть всё, чтобы считать фундаментные болты по ГОСТ по СП 513.1 325 800.2022.
И снова СП 43
Осталось только одна проблема — динамика. Вывернем формулы СП 43 так, чтобы коэффициенты остались с одной из сторон и получим граничные коэффициенты использования. Для всех анкерных креплений:
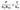
где P – расчетная нагрузка на болт
An – площадь поперечного сечения болта нетто
Rba – расчетное сопротивление стали фундаментного болта растяжению
k0 – коэффициент, учитывающий динамичность нагрузок.
Таблица 6 — Значение коэффициента k0 в зависимости от типа нагрузки
Тип нагрузкиЗначение коэффициента k0
Динамическая1.35
Ветровая1.18
Статическая1.05
При действии динамических нагрузок:
где P – расчетная нагрузка на болт
An – площадь поперечного сечения болта нетто
Rba – расчетное сопротивление стали фундаментного болта растяжению
α – коэффициент, учитывающий число циклов нагружения
χ – коэффициент нагрузки болта
μ – коэффициент, учитывающий диаметр болта.
Таблица 7 – Значение коэффициентов μ, α и χ
Коэффициент μ Диаметр болтаЗначение μКоэффициент α Число циклов нагруженияЗначение αКоэффициент χ Конструкция болтаЗначение χ
M161.050 0003.15С отгибом0.40
M20, M241.1200 0002.25С плитой0.40
M30, M361.3800 0001.57Прямой0.60
M42, M481.62 000 0001.25Конический0.55
M56, M641.85 000 0001.00--
ФИНАЛ
Осталось слепить франкенштейна из положений СП 513.1 325 800.2022, СП 43.13 330.2012 и Пособия по проектированию анкерных креплений строительных конструкций и оборудования.
При действии статических и ветровых нагрузок максимальный коэффициент использования определяется по формуле:
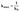
где k0 – коэффициент, учитывающий динамичность нагрузок (см. таблицу 6).
При действии динамических нагрузок, максимальный коэффициент использования определяется по формуле:
При растяжении фундаментные болты следует проверять по формуле:
где P – расчетная нагрузка на болт
Nult – расчетная несущая способность анкера на растяжение
γNs=1.25 – коэффициент надежности по стали анкера
Nn.s=N0.u.s – нормативное значение силы сопротивления анкера при разрушении по стали от растяжения
Ryn – нормативное сопротивление стали фундаментного болта растяжению
Abn – площадь поперечного сечения болта нетто
Rba – расчетное сопротивление стали фундаментного болта растяжению
kmax – максимальный коэффициент использования.
При сдвиге без момента фундаментные болты следует проверять по формуле:
где Q – расчетная нагрузка на болт
Vult – расчетная несущая способность анкера на сдвиг
γVs=1.25 – коэффициент надежности по стали анкера
Vn.s=Vu.s – нормативное значение силы сопротивления анкера при сдвиге
Ryn – нормативное сопротивление стали фундаментного болта растяжению
A – площадь поперечного сечения болта по плоскости среза
kmax – максимальный коэффициент использования.
При сдвиге с учетом момента фундаментные болты следует проверять по формуле:
где Q – расчетная нагрузка на болт
Vult – расчетная несущая способность анкера на сдвиг
γVs=1.25 – коэффициент надежности по стали анкера
Vnm.s – нормативное значение силы сопротивления анкера при сдвиге с учетом момента
kmax – максимальный коэффициент использования.
Нормативное значение силы сопротивления анкера при сдвиге с учетом момента определяется по формуле:
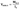
где Mn.s – приведенная величина предельного изгибающего момента по стали с учетом комбинированного воздействия
ls – плечо поперечной силы.
Приведенная величина предельного изгибающего момента определяется по формуле:
где M0n.s – нормативное значение предельного изгибающего момента
P – расчетная нагрузка на болт
Nult – расчетная несущая способность анкера на растяжение
γNs=1.25 – коэффициент надежности по стали анкера
Nn.s=N0.u.s – нормативное значение силы сопротивления анкера при разрушении по стали от растяжения
Ryn – нормативное сопротивление стали фундаментного болта растяжению
Abn – площадь поперечного сечения болта нетто
Rba – расчетное сопротивление стали фундаментного болта растяжению
kmax – максимальный коэффициент использования.
Нормативное значение предельного изгибающего момента определяется по формуле:
где Ryn – нормативное сопротивление стали фундаментного болта
W – момент сопротивления сечения фундаментного болта
γVs=1.25 – коэффициент надежности по стали анкера.
Наконец, поставим всё обратно и получим формулу проверки прочности анкерного болта при действии сдвига с учетом дополнительных моментов:
где Q – расчетная нагрузка на болт
Vult – расчетная несущая способность анкера на сдвиг
ls – плечо поперечной силы
γVs=1.25 – коэффициент надежности по стали анкера
Ryn – нормативное сопротивление стали фундаментного болта растяжению
W – момент сопротивления сечения фундаментного болта
P – расчетная растягивающая нагрузка на болт
Rba – расчетное сопротивление стали фундаментного болта растяжению
Abn – площадь поперечного сечения болта нетто
kmax – максимальный коэффициент использования.
При совместном действии растяжения и сдвига фундаментные болты следует проверять по формуле:
где P – расчетная растягивающая нагрузка на болт
Q – расчетная поперечная нагрузка на болт
Abn – площадь поперечного сечения болта нетто
Rba – расчетное сопротивление стали фундаментного болта растяжению
Vult – расчетная несущая способность анкера на сдвиг
kmax – максимальный коэффициент использования.
Итого
Три дня, три человека и более двадцати различных нормативных документов, статей и книг. Осталось всё это как-то рассказать эксперту при защите проекта.
Если остались вопросы — пишите их нам в социальных сетях.


Автор статьи:

Блинов Сергей

Инженер-конструктор

ПУБЛИКАЦИИ
Определение расчетных длин в любых ситуациях
— Все еще мучаетесь с определением расчетных длин?
— Тогда мы идем к Вам!

Мы постарались сделать так чтобы после этого вебинара у вас не осталось вопросов как определить расчетные длины даже в самых сложных ситуациях.